Merge Sort: Your Sorting Companion

Sorting is a fundamental operation in computer science and is used in various real-world applications. One of the popular sorting algorithms is Merge Sort, which is efficient and easy to implement. In this blog post, we'll explore Merge Sort, how it works, and its real-world examples.

What is Merge Sort?

Merge Sort is a Divide and Conquer algorithm that sorts an array or a list by dividing it into two halves, sorting each half separately, and then merging the sorted halves back together. The sorting is done recursively until the base case is reached, where the array or list contains only one element.

The algorithm was invented by John von Neumann in 1945, and it is a stable, comparison-based algorithm. Merge Sort has a time complexity of O(n log n), which makes it faster than other popular sorting algorithms such as Bubble Sort and Insertion Sort.

How does Merge Sort work?

The Merge Sort algorithm works as follows:

1. Divide the unsorted array or list into two halves.

2. Recursively sort each half.

3. Merge the two sorted halves back together.

The base case of the recursion is when the array or list contains only one element, which is already sorted. The merging process is done by comparing the first elements of each half and placing the smaller one in the sorted array or list. This process is repeated until all the elements are merged into the sorted array or list.

Step-by-step illustration of how the Merge Sort algorithm works, showing how it recursively sorts and merges data to achieve optimal results:

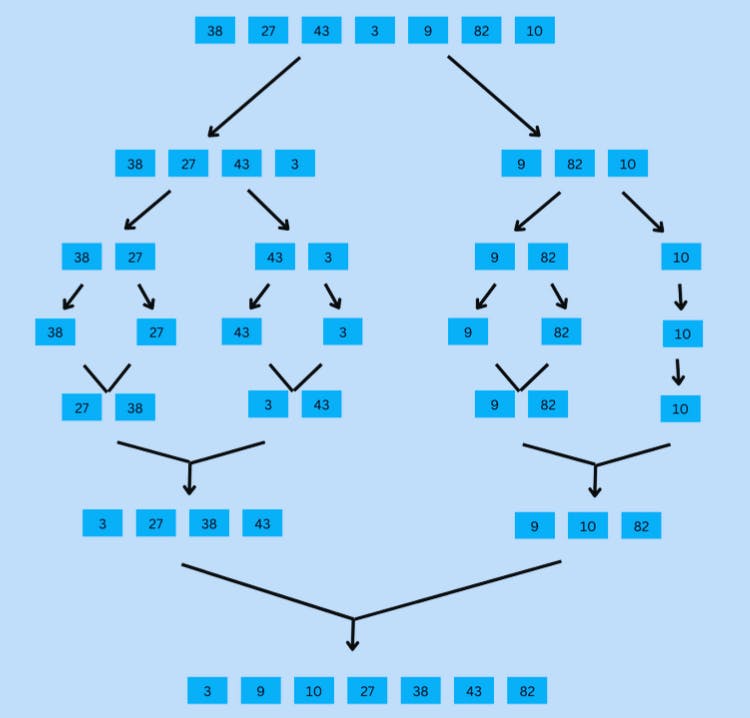
Example

Let's take an example to understand Merge Sort better. Consider an unsorted array of integers:

[38, 27, 43, 3, 9, 82, 10]

The Merge Sort algorithm works as follows:

1. Divide the array into two halves: [38, 27, 43, 3] and [9, 82, 10]

2. Recursively sort each half:

   1. Divide the first half into two halves: [38, 27] and [43, 3]

   2. Recursively sort each half:

      1. Divide the first half into two halves: [38] and [27] (base case reached)

      2. Merge the two halves back together: [27, 38]

   3. Recursively sort the second half:

      1. Divide the first half into two halves: [43] and [3] (base case reached)

      2. Merge the two halves back together: [3, 43]

   4. Merge the two sorted halves back together: [3, 27, 38, 43]

3. Recursively sort the second half:

   1. Divide the first half into two halves: [9, 82] and [10]

   2. Recursively sort the second half:

      1. Divide the first half into two halves: [9] and [82] (base case reached)

      2. Merge the two halves back together: [9, 82]

   3. Merge the two sorted halves back together: [9, 10, 82]

4. Merge the two sorted halves back together: [3, 9, 10, 27, 38, 43, 82]

The sorted array is [3, 9, 10, 27, 38, 43, 82].

C++ Implementation:

#include <iostream>
using namespace std;

// Time Complexity --> O(n log n)
// Auxilary Space --> O(n)

void merge(int arr[], auto start, auto end){
    auto mid = start + (end - start) / 2;
    int i = start;
    int j = mid + 1;

    int newSize = (end - start) + 1;
    int *newArr = new int[newSize];
    int k = 0;

    while(i <= mid && j <= end){
        if(arr[i] <= arr[j]){
            newArr[k++] = arr[i++];
        }
        else{
            newArr[k++] = arr[j++];
        }
    }

    while(i <= mid){
        newArr[k++] = arr[i++];
    }
    while(j <= end){
        newArr[k++] = arr[j++];
    }

    k = 0;
    for(int i = start; i <= end; i++){
        arr[i] = newArr[k++];
    }

    delete []newArr;
}

void mergeSort(int arr[], auto start, auto end){
    if(start >= end) return;

    int mid = start + (end - start) / 2;
    mergeSort(arr, start, mid);
    mergeSort(arr, mid + 1, end);
    merge(arr, start, end);
}

int main() { 
    int arr[] = {2, 9, 6, 1, 18, 4};
    auto n = sizeof(arr) / sizeof(int);
    mergeSort(arr, 0, n - 1);

    // Printing the sorted array
    for(int i = 0; i < n; i++){
        cout << arr[i] << " ";
    }
    cout << endl;
    return 0;
}

Real-world examples

Merge Sort is used in various real-world applications where sorting is required. Some examples include:

• Database Sorting

Databases are used to store large amounts of data in an organized manner. To access the data efficiently, it is important to keep the data sorted. Merge Sort is a popular algorithm used to sort databases. It is an efficient algorithm for sorting large datasets and can handle different data types.

• Parallel Processing

Parallel processing is a technique used to process large amounts of data by dividing the data into smaller chunks and processing them simultaneously. Merge Sort is an ideal algorithm for parallel processing because it can easily be divided into smaller subproblems that can be processed in parallel. The sorted subproblems can then be merged back together to produce the final sorted dataset.

• Network Routing

Network routing is a process used to find the best path for data to travel through a network. The process involves sorting large amounts of data to determine the best path. Merge Sort is a popular algorithm used for network routing because it can efficiently sort large datasets and find the best path quickly.

• Multimedia Sorting

Multimedia files, such as images and videos, are large files that require sorting to access the data efficiently. Merge Sort is an ideal algorithm for sorting multimedia files because it can handle different data types and efficiently sort large datasets.

In summary, Merge Sort is a reliable and efficient algorithm that is widely used in many industries. Its ability to handle large datasets and different data types makes it a popular choice for developers and engineers who need to sort large amounts of data quickly and accurately.

Conclusion:

I hope this article has helped you understand Merge Sort and its applications in real-world scenarios. If you have any questions or comments, feel free to leave them below.

Thank you for taking the time to read this article. If you found it useful, please consider sharing it with your friends and colleagues. Your support is greatly appreciated!